Uncrashable languages aren't

Making buggy situations unrepresentable

Programs have bugs. Both creators and end-users of software dislike bugs. Businesses paying for software development dislike bugs. It’s no wonder that, as the role of software in the world expands, we’ve become very interested in minimizing occurrences of bugs.

One way of reducing bugs is via process: making sure that critical code is tested to the greatest practical extent. Another way is via construction: making sure that buggy code is not representable. This could be achieved by making such code unexpressible in the syntax of a language, or having it fail the compiler’s type check.

There are two new programming languages that take a principled stance on the side of non-representability, by preventing code from crashing wantonly: Elm and Pony.

Elm does this by eliminating exceptions from language semantics and forcing the programmer to handle all branches of sum types (i.e your code has to cover all representable states that it might encounter).

Pony does this by allowing anonymous exceptions (the error operator), but forcing the programmer to deal with them at some point. All functions – apart from those which are explicitly marked as capable of throwing errors – MUST be total and always return a value.

A small aside about division by zero

Elm used to crash when you tried to divide by zero. Now (I tried version 0.19), it returns 0 for integer division and Infinity for floating-point division. The division functions are therefore total.

> 5.0 / 0.0
Infinity : Float
> 5 // 0
0 : Int
> remainderBy 5 0
0 : Int
> modBy 5 0
0 : Int

Pony also returns zero when zero is the divisor.

actor Main                                        //  This code prints:
  new create(env: Env) =>                         //  0
   env.out.print((U32(1) / U32(0)).string())

However, Pony also provides partial arithmetic operators (/? for division, +? for addition, below), for when you explicitly need integer over/underflows and division-by-zero to be illegal:

actor Main                                         //  This code prints:
  new create(env: Env) =>                          //  div by zero
    try U32(1) /? U32(0)                           //  overflow
    else env.out.print("div by zero")              //  0
    end                                            //  0
    try U8(255) +? U8(1)
    else env.out.print("overflow")
    end
   env.out.print((U32(1) / U32(0)).string())
   env.out.print((U8(255) + U8(1)).string())

While returning ‘0’ for divison-by-zero is a controversial topic (yet silent integer overflows somehow don’t generate the same debate), I think it’s reasonable to view this compromise as the necessary cost of eliminating crashes in our code. More interesting is this: we have just made a tradeoff between eliminating crashes and wrong results. Having a total division function eliminates crashes at the cost of allowing wrong results to propagate. Let’s dig into this a bit more.

Bugs and the bottom type

Taxonomy is supposed to be the lowest form of science, but let’s indulge and distinguish two main types of program misbehavior:

1) A program (or function) produces output which does not match the programmer’s intent, design, or specification;

2) A program (or function) fails to produce output (e.g. freezes or crashes)

I hope you’ll agree that eliminating ‘bugs’ caused by the first type of error is not an easy feat, and probably not within the scope of a language runtime or compiler. Carefully designing your data structures to make illegal states unrepresentable may go a long way towards eliminating failures of this kind, as will a good testing regimen. Let’s not delve deeper into this category and focus on the second one: functions that crash and never return.

The wikipedia article on the Bottom Type makes for an intersting read. It’s nice to conceive of ⊥ as a hole in the program, where execution stops and meaning collapses. Since the bottom type is a subtype of every type, theoretically any function can return the ‘bottom value’ — although returning the ‘bottom value’ acutally means never returning at all.

My claim is that while some languages, like Haskell or Rust, might explicitly embrace the existence of ⊥, languages that prevent programmers from ‘invoking’ the bottom type will always contain inconsistencies (I’m leaving dependently-typed languages out of this). Below are two examples.

Broken promises and infinite loops

Elm’s promise is that an application written in Elm will never crash, unless there is a bug in the Elm runtime. There are articles out there that enumerate the various broken edge-cases (regexp, arrays, json decoding), but these cases can arguably be construed as bugs in the runtime or mistakes in library API design. That is, these bugs do not mean that Elm’s promise is for naught.

However, if you think about it, an infinite loop is a manifestation of the bottom type just as much as an outright crash, and such a loop is possible in all Turing-complete languages.

Here’s a legal Elm app that freezes:

import Browser
import Html exposing (Html, button, div, text)
import Html.Events exposing (onClick)

main =
  Browser.sandbox { init = 0, update = update, view = view }

type Msg = Increment | Decrement

add : Int -> Int
add n =
  add (n+1)

update msg model =
  case msg of
    Increment ->
      add model

    Decrement ->
      model - 1

view model =
  div []
    [ button [ onClick Decrement ] [ text "-" ]
    , div [] [ text (String.fromInt model) ]
    , button [ onClick Increment ] [ text "+" ]
    ]

What will happen when you click the + button in the browser? This is what:

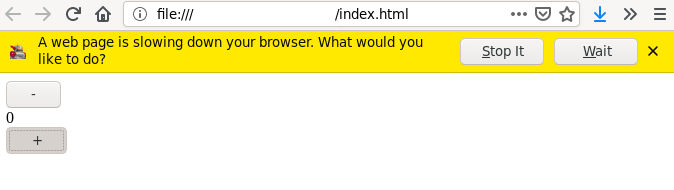
The loop is hidden in the add function, which never actually returns an Int. Its true return type, in this program, is precisely ⊥. Without explicitly crashing-and-stopping, we’ve achieved the logical (and type-systematic) equivalent: a freeze.

Galloping forever and ever

The Pony language is susceptible to a similar trick, but we’ll have to be a bit more crafty. First of all, Pony does indeed allow the programmer to ‘invoke’ the Bottom Type, by simply using the keyword error anywhere in a function body. Using this keyword (or calling a partial function) means that we, the programmer, now have a choice to make:

1) Use try/else to handle the possibility of error, and return a sensible default value

2) Mark this function as partial ?, and force callers to deal with the possibility of the Bottom Type rearing its head.

However, we can craft a function that spins endlessly, never exiting, and thus ‘returning’ the Bottom Type, without the compiler complaining, and without having to annotate it as partial.

Interestingly enough, naïve approaches are optimized away by the compiler, producing surprising result values instead of spinning forever:

actor Main
  new create(env: Env) =>
    let x = spin(false)
    env.out.print(x.string())

  fun spin(n: Bool): Bool =>
    spin(not n)

Before you run this program, think about what, if anything, it should output. Then, run it and see. Seems like magic to me, but I’m guessing this is LLVM detecting the oscillation and producing a ‘sensible’ value.

We can outsmart the optimizer by farming out the loop to another object:

actor Main
  new create(env: Env) =>
    let t: TarpitTrap = TarpitTrap
    let result = t.spin(true)
    env.out.print(result.string())

class TarpitTrap
  fun spin(n: Bool): Bool =>
    if n then spin(not n)
    else spin(n)
    end

Now, this program properly freezes forever, as intended. Of course this is just a contrived demonstration, but one can imagine an analogous situation happening at run-time, for example when parsing tricky (or malicious) input data.

The snake in the garden

While I enjoy working both in Elm and Pony, I’m not a particular fan of these languages’ hard-line stance on making sure programs never crash. As long as infinite loops are expressible in the language, the Bottom Type cannot be excised.

Even without concerns somewhat external to our programming language runtime, such as memory constraints, FFIs, syscalls, or the proverbial admin pulling the plug on our machine (did this really used to happen?), the humble infinite loop ensures that non-termination can never be purged from our (non-dependently-typed) program.

Instead of focusing on preventing crashes in the small, I think we, as programmers, should embrace failure and look at how to deal with error from a higher-level perspective, looking at processes, machines, and entire systems. Erlang and OTP got this right so many years ago. Ensuring the proper operation of a system despite failure is a much more practical goal than vainly trying to expel the infinitely-looping snake from our software garden.